Advertisements
Advertisements
प्रश्न
In following figure , AB , a chord of the circle is of length 18 cm. It is perpendicularly bisected at M by PQ.
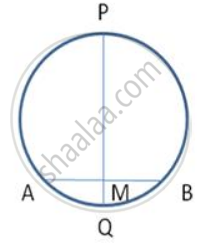
उत्तर
Given : AB = 18 cm , MQ = 3 cm
To find : PQ
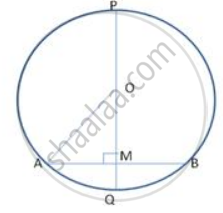
OQ = OA = r cm (say)
∴ OM = OQ = MQ = (r - 3) cm
AM = MB = 9 cm (PQ ⊥ AB)
In right Δ OMA ,
OM2 + MA2 = OA2
⇒ (r - 3)2 + 92 = r2
⇒ r2 - 6r + 9 + 81 = r2
⇒ 6r = 90
⇒ r = 15 cm
PQ = 2r
(Perpendicular bisector of a chord passes through the centre of the circe)
PQ = 2(15)
PQ = 30 cm
APPEARS IN
संबंधित प्रश्न
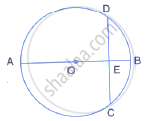
The figure given below, shows a circle with centre O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4cm, find the radius of the circle.
Two circle with centres A and B, and radii 5 cm and 3 cm, touch each other internally. If the perpendicular bisector of the segment AB meets the bigger circle in P and Q; find the length of PQ.
In Δ ABC, the perpendicular from vertices A and B on their opposite sides meet (when produced) the circumcircle of the triangle at points D and E respectively. Prove that: arc CD = arc CE
The given figure shows two circles with centres A and B; and radii 5 cm and 3 cm respectively, touching each other internally. If the perpendicular bisector of AB meets the bigger circle in P and Q, find the length of PQ.

The radius of a circle is 17.0 cm and the length of the perpendicular drawn from its center to a chord is 8.0 cm.
Calculate the length of the chord.
AB and CD are two equal chords of a circle with center O which intersect each other at a right angle at point P.
If OM ⊥ AB and ON ⊥ CD;
show that OMPN is a square.
AB is a diameter of a circle with centre C = (- 2, 5). If A = (3, – 7). Find
(i) the length of radius AC
(ii) the coordinates of B.
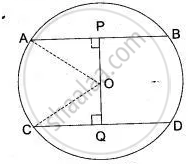
In Fig. O is the centre of the circle with radius 5 cm. OP⊥ AB, OQ ⊥ CD, AB || CD, AB = 8 cm and CD = 6 cm. Determine PQ.
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, find the radius of the circle.
AB, CD are parallel chords of a circle 7 cm apart. If AB = 6 cm, CD = 8 cm, find the radius of the circle.
