Advertisements
Advertisements
प्रश्न
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

उत्तर
Since arc AB makes ∠ AOB at the centre and ∠ APB = 500 on the remaining part of the circle.
∠ AOB = 2 ∠ APB
∠ AOB = 2(50) = 100°
AO= OB = x (radii of same circle)
In Δ AOB
∠ AOB + ∠ BAO + ∠ ABO = 180
180 + x + x = 180
2x = 80
x = 40
∴ ∠ OAB = 40°
APPEARS IN
संबंधित प्रश्न
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

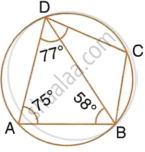
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG = 108° and O is the centre of the circle, find :
- angle BCT
- angle DOC

ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
In Fig. ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF || DC.
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
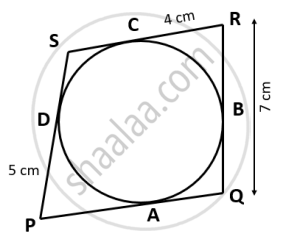
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ: