Advertisements
Advertisements
प्रश्न
Prove that the quadrilateral formed by angle bisectors of a cyclic quadrilateral ABCD is also cyclic.
उत्तर
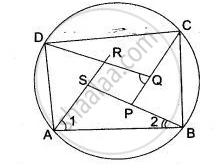
Given: In cyclic ABCD the bisectors formed a quadrilateral ABCD.
To prove: PQRS is a cyclic quadrilateral.
Proof: In cyclic quadrilateral ABCD, AR and BS be the bisectors of ∠A and ∠B.
So, ∠ 1 = ∠ A/2 and ∠ 2 = ∠ B/2
In Δ ASB, ∠ RSP is the exterior angle
So ∠ RSP = ∠1 + ∠2
∠ RSP = `"∠A"/2 + "∠B"/2` ....(i)
Similarly, ∠ PQR = `"∠C"/2 + "∠D"/2` ....(ii)
Adding (i) and (ii),
∠ PQR + ∠ RSP = `1/2`(∠A + ∠B + ∠C + ∠D)
= `1/2` x 360° = 180°
∠ PQR + ∠ RSP = 180°
But these are the opposite angles of quadrilateral PQRS
Hence PQRS is a cyclic quadrilateral.
Hence proved.
APPEARS IN
संबंधित प्रश्न
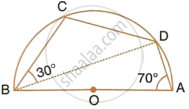
In the given figure, C and D are points on the semi-circle described on AB as diameter. Given angle BAD = 70° and angle DBC = 30°, calculate angle BDC.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
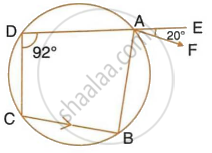
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC=120°.
Calculate: ∠ BED.
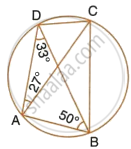
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
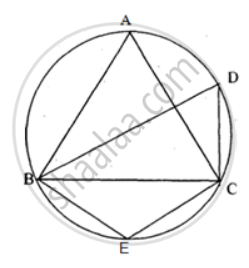
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

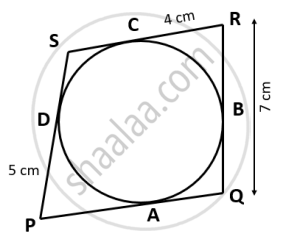
In the given figure, the sides of the quadrilateral PQRS touches the circle at A, B, C and D. If RC = 4 cm, RQ = 7 cm and PD = 5 cm. Find the length of PQ: