Advertisements
Advertisements
प्रश्न
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
उत्तर
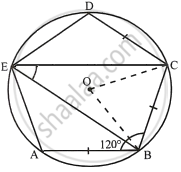
i. Join OC and OB.
AB = BC = CD and ∠ABC = 120°
∴ ∠BCD = ∠ABC = 120°
OB and OC are the bisectors of ∠ABC and ∠BCD respectively.
∴ ∠OBC = ∠BCO = 60°
In ΔBOC,
∠BOC = 180° – (∠OBC + ∠BOC)
`=>` ∠BOC = 180° – (60° + 60°)
`=>` ∠BOC = 180° – 120° = 60°
Arc BC subtends ∠BOC at the centre and ∠BEC at the remaining part of the circle.
∴ `∠BEC = 1/2 ∠BOC = 1/2 xx 60^circ = 30^circ`
ii. In cyclic quadrilateral BCDE,
∠BED + ∠BCD = 180°
`=>` ∠BED + 120° = 180°
∴ ∠BED = 180° – 120° = 60°
APPEARS IN
संबंधित प्रश्न
ABCD is a quadrilateral inscribed in a circle, having ∠ = 60°; O is the center of the circle.
Show that: ∠OBD + ∠ODB =∠CBD +∠CDB.
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

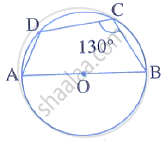
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA
If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
In following figure , Δ PQR is an isosceles teiangle with PQ = PR and m ∠ PQR = 35° .Find m ∠ QSR and ∠ QTR

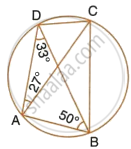
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
In the given below figure,
∠ BAD = 65°
∠ ABD = 70°
∠ BDC = 45°
Find: (i) ∠ BCD, (ii) ∠ ADB.
Hence show that AC is a diameter.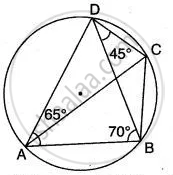
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
