Advertisements
Advertisements
प्रश्न
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
उत्तर
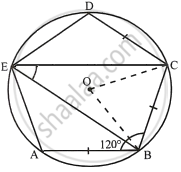
i. Join OC and OB.
AB = BC = CD and ∠ABC = 120°
∴ ∠BCD = ∠ABC = 120°
OB and OC are the bisectors of ∠ABC and ∠BCD respectively.
∴ ∠OBC = ∠BCO = 60°
In ΔBOC,
∠BOC = 180° – (∠OBC + ∠BOC)
`=>` ∠BOC = 180° – (60° + 60°)
`=>` ∠BOC = 180° – 120° = 60°
Arc BC subtends ∠BOC at the centre and ∠BEC at the remaining part of the circle.
∴ `∠BEC = 1/2 ∠BOC = 1/2 xx 60^circ = 30^circ`
ii. In cyclic quadrilateral BCDE,
∠BED + ∠BCD = 180°
`=>` ∠BED + 120° = 180°
∴ ∠BED = 180° – 120° = 60°
APPEARS IN
संबंधित प्रश्न
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.

Find:
- ∠CAD
- ∠CBD
- ∠ADC
ABCD is a cyclic quadrilateral, AB and DC are produced to meet in E. Prove that ΔEBC ≅ ΔEDA.
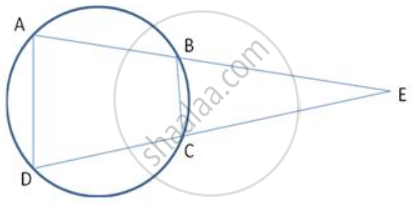
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
In following fig., O is the centre of the circle. Find ∠ CBD.
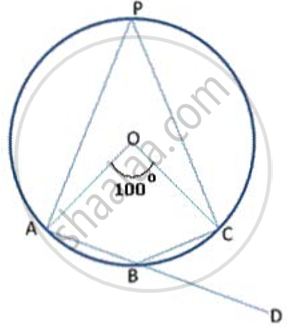
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.

If ∠ CAB = 34° , find : ∠ CQB
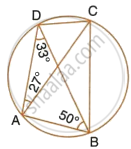
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.
The diagonals of a cyclic quadrilateral are at right angles. Prove that the perpendicular from the point of their intersection on any side when produced backward bisects the opposite side.
