Advertisements
Advertisements
प्रश्न
Prove that the angles bisectors of the angles formed by producing opposite sides of a cyclic quadrilateral (provided they are not parallel) intersect at right triangle.
उत्तर
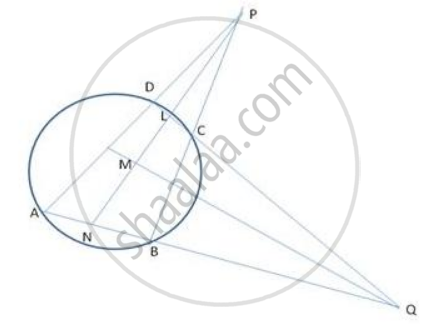
Here, ABCD is a cyclic quadrilateral. PM is bisector of ∠ APB and QM is bisector of ∠ AQD
In Δ PDL and Δ PBN, ∠ 1=∠ 2 (PM is a bisector of LP)
∠ 3 = ∠ 9 (exterior angle of cydic quad. = interior opposite angle)
∴ ∠ 4 = ∠ 7
But, ∠ 4 = ∠ 8 (vertical opposite angles)
∴ ∠ 7 = ∠ 8
Now in Δ QMN and Δ QML
∠ 7 = ∠ 8 (proved above)
∠ S = ∠ 6 (QM is bisector of Q)
∴ Δ QMN ~ Δ QML
⇒ ∠ QMN and ∠ QML
But, ∠ QMN + ∠ QML = 180°
∴ ∠ QMN = ∠ QML = 90°
Hence, ∠ PMQ = 90 °
APPEARS IN
संबंधित प्रश्न
In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

In the given figure, AB = AC. Prove that DECB is an isosceles trapezium.
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
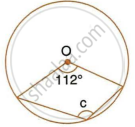
In the following figure, O is the centre of the circle. Find the values of a, b and c.
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

