Advertisements
Advertisements
प्रश्न
Bisectors of vertex angles A, B, and C of a triangle ABC intersect its circumcircle at the points D, E and F respectively. Prove that angle EDF = 90° – `1/2` ∠A.
उत्तर
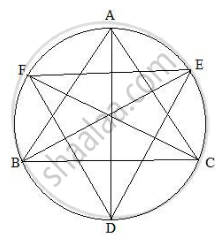
We have,
Given that, BE is the bisector of B.
`therefore angle ABE = (angleB)/2`
`angleADE = angleABE` ...(Angles in the same segment for chord AF)
Similarly, `angle ACF = angleADF = (angleC)/2` ...(Angle in the same segment for chord AF)
`angleD = angleADE + angleADF`
`angleD = (angleB)/2 + (angleC)/2`
= `1/2 (angleB + angleC)`
= `1/2 (180^circ - angleA)` ...`(∴ angleA + angleB + angleC = 180^circ)`
`angleD = 90^circ - (angleA)/2`
APPEARS IN
संबंधित प्रश्न
In the figure, given below, find:
- ∠BCD,
- ∠ADC,
- ∠ABC.
Show steps of your working.

ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°; find ∠BAC.

In the following figure,
- if ∠BAD = 96°, find ∠BCD and ∠BFE.
- Prove that AD is parallel to FE.

In cyclic quadrilateral ABCD, ∠A = 3∠C and ∠D = 5∠B. Find the measure of each angle of the quadrilateral.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle ABC = 120°.
Calculate:
- ∠BEC
- ∠BED
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B. If ∠A : ∠B = 2 : 1; find angles A and B.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.
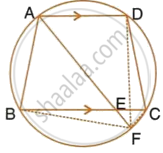
If the bisector of angle A meets BC at point E and the given circle at point F, prove that:
- EF = FC
- BF = DF
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
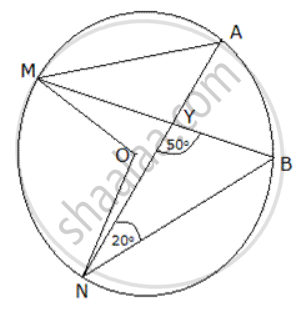
MABN are points on a drde having centre O. AN and MB cut at Y. If ∠ NYB = 50" and ∠ YNB = 200, find ∠ MAN and reflex angle MON.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

