Advertisements
Advertisements
प्रश्न
In the figure, AB is the chord of a circle with centre O and DOC is a line segment such that BC = DO. If ∠C = 20°, find angle AOD.

उत्तर
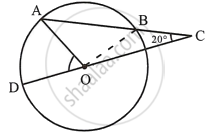
Join OB,
In ΔOBC,
BC = OD = OB ...(Radii of the same circle)
∴ ∠BOC = ∠BCO = 20°
And Ext. ∠ABO = ∠BCO + ∠BOC
`=>` Ext. ∠ABO = 20° + 20° = 40° ...(i)
In ΔOAB,
OA = OB ...(Radii of the same circle)
∴ ∠OAB = ∠OBA = 40° ...(From (i))
∠AOB = 180° – ∠OAB – ∠OBA
`=>` ∠AOB = 180° – 40° – 40° = 100°
Since DOC is a straight line
∴ ∠AOD + ∠AOB + ∠BOC = 180°
`=>` ∠AOD + 100° + 20° = 180°
`=>` ∠AOD = 180° – 120°
`=>` ∠AOD = 60°
APPEARS IN
संबंधित प्रश्न
The length of common chord of two intersecting circles is 30 cm. If the diameters of these two circles be 50 cm and 34 cm, calculate the distance between their centres.
In the figure, AB is common chord of the two circles. If AC and AD are diameters; prove that D, B and C are in a straight line. O1 and O2 are the centers of two circles.

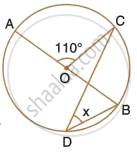
In the figure, given alongside, AOB is a diameter of the circle and ∠AOC = 110°. Find ∠BDC.
The diameter and a chord of a circle have a common end-point. If the length of the diameter is 20 cm and the length of the chord is 12 cm, how far is the chord from the centre of the circle?
In the given figure, QAP is the tangent at point A and PBD is a straight line.
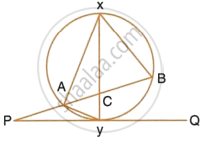
If ∠ACB = 36° and ∠APB = 42°, find:
- ∠BAP
- ∠ABD
- ∠QAD
- ∠BCD
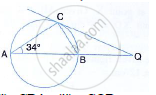
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.
If ∠CAB = 34°, Find : ∠CBA
Prove that the line segment joining the midpoints of two parallel chords of a circle passes through its centre.
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In following figure . O is the centre of the circle. Find ∠ BAC.
In the given figure, AB and CD are two equal chords of a circle, with centre O. If P is the mid-point of chord AB, Q is the mid-point of chord CD and ∠POQ = 150°, find ∠APQ.