Advertisements
Advertisements
प्रश्न
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
उत्तर
∠ B = 65°( given)
∠ B + ∠ D = 180 (Opposite angles of a cydic quadrilateral)
65 + ∠ D = 180
∠ D = 115
Also, AB || CD
∴ ∠ B + ∠ C = 180 (Sum of angles on same side of transversal)
∠ C = 180 - 65 = 115
Again, ∠ A+ ∠ C = 180° (Opposite angles of a cyclic quadrilateral
∠ A = 180 - 115 = 65°
APPEARS IN
संबंधित प्रश्न
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of:
- ∠BCD
- ∠BOD
- ∠OBD

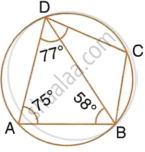
In the figure, given below, ABCD is a cyclic quadrilateral in which ∠BAD = 75°; ∠ABD = 58° and ∠ADC = 77°. Find:
- ∠BDC,
- ∠BCD,
- ∠BCA.
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
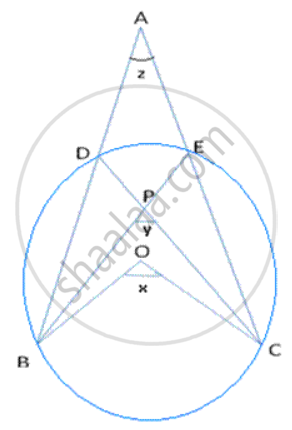
In following fig., O is the centre of the circle, prove that ∠x =∠ y + ∠ z.
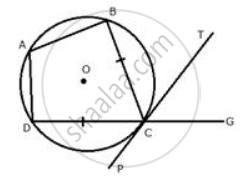
In the figure, ABCD is a cyclic quadrilateral with BC = CD. TC is tangent to the circle at point C and DC is produced to point G. If angle BCG=108° and O is the centre of the circle, find: angle DOC
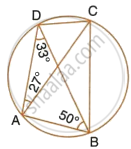
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate : ∠DCB.
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
In the given below the figure, O is the centre of the circle and ∠ AOC = 160°. Prove that 3∠y - 2∠x = 140°.

