Advertisements
Advertisements
Question
In a cyclic quadrilateral ABCD , AB || CD and ∠ B = 65° , find the remaining angles.
Solution
∠ B = 65°( given)
∠ B + ∠ D = 180 (Opposite angles of a cydic quadrilateral)
65 + ∠ D = 180
∠ D = 115
Also, AB || CD
∴ ∠ B + ∠ C = 180 (Sum of angles on same side of transversal)
∠ C = 180 - 65 = 115
Again, ∠ A+ ∠ C = 180° (Opposite angles of a cyclic quadrilateral
∠ A = 180 - 115 = 65°
APPEARS IN
RELATED QUESTIONS
In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T
1) Prove ΔTPS ~ ΔTRQ.
2) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm
3) Find the area of quadrilateral PQRS if the area of ΔPTS = 27 cm2.
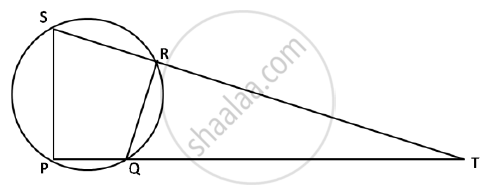
In the given figure, SP is bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that : SQ = SR.

In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
If two non-parallel sides of a trapezium are equal, it is cyclic. Prove it. Or An isosceles trapezium is always cyclic. Prove it.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Prove that the points B, C, E and D are concyclic.
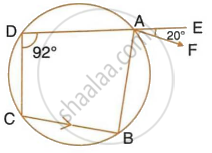
In the given figure, ABCD is a cyclic quadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ADC = 92°, ∠FAE = 20°; determine ∠BCD. Give reason in support of your answer.
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

In a cyclic quadrialteral ABCD , if m ∠ A = 3 (m ∠C). Find m ∠ A.
In fig., O is the centre of the circle and ∠ AOC = 1500. Find ∠ ABC.
In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

