Advertisements
Advertisements
Question
In the given figure, PAT is tangent to the circle with centre O at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that:
- ∠BAP = ∠ADQ
- ∠AOB = 2∠ADQ
- ∠ADQ = ∠ADB

Solution
i. Since PAT || BC
∴ ∠PAB = ∠ABC (Alternate angles) ...(i)
In cyclic quadrilateral ABCD,
Ext ∠ADQ = ∠ABC ...(ii)
From (i) and (ii)
∠PAB = ∠ADQ
ii. Arc AB subtends ∠AOB at the centre and ∠ADB at the remaining part of the circle.
∴ ∠AOB = 2∠ADB
`=>` ∠AOB = 2∠PAB ...(Angles in alternate segments)
`=>` ∠AOB = 2∠ADQ ...(Proved in (i) part)
iii. ∴ ∠BAP = ∠ADB ...(Angles in alternate segments)
But ∠BAP = ∠ADQ ...(Proved in (i) part)
∴ ∠ADQ = ∠ADB
APPEARS IN
RELATED QUESTIONS
PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate:
1) ∠QRS
2) ∠RQS
3) ∠PRQ

Two circles intersect in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that A, Q, B and T lie on a circle.
In following figure , O is the centre of the circle. If ∠ APB = 50° then find ∠ AOB and ∠ OAB.

In triangle ABC, AB = AC. A circle passing through B and c intersects the sides AB and AC at D and E respectively. Prove that DE || BC.
The bisectors of the opposite angles A and C of a cydic quadrilateral ABCD intersect the cirde at the points E and F, respectively. Prove that EF is a diameter of the circle.
In following figure.,ABCD is a cyclic quadrilateral . If ∠ BCD = 100° and ∠ ABD = 70° , find ∠ ADB.
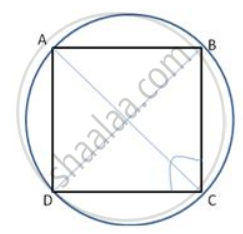
In the following figure, O is the centre of the circle. Find the values of a, b and c.
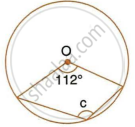
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate : ∠BAC
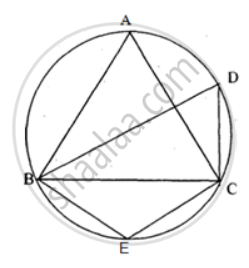
In ABCD is a cyclic quadrilateral; O is the centre of the circle. If BOD = 160°, find the measure of BPD.
