Advertisements
Advertisements
Question
Solution
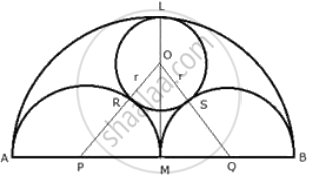
Let O, P and Q be the centers of the circle and semicircle.
Join OP and OQ.
OR = OS = r
And `AP = PM = MQ = QB = (AB)/4`
Now, `OP = OR + RP = r + (AB)/4` ...(Since PM = RP = radii of same circle)
Similarly, `OQ = OS + SQ = r + (AB)/4`
`OM = LM - OL = (AB)/2 - r`
Now in right ΔOPM,
OP2 = PM2 + OM2
`=> (r + (AB)/4)^2 = ((AB)/4)^2 + ((AB)/2 - r)^2`
`=> r^2 + (AB^2)/16 + (rAB)/2 = (AB^2)/16 + (AB^2)/4 + r^2 - rAB`
`=> (rAB)/2 = (AB^2)/4 - rAB`
`=> (AB^2)/4 = (rAB)/2 + rAB`
`=> (AB^2)/4 = (3rAB)/2`
`=> (AB)/4 = 3/2 r`
`=> AB = 3/2 rxx 4 = 6r`
Hence AB = 6 × r
APPEARS IN
RELATED QUESTIONS
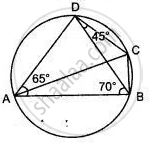
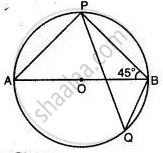
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
Prove that the parallelogram, inscribed in a circle, is a rectangle.
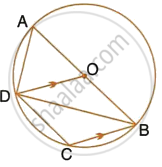
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
In the figure, given alongside, AB || CD and O is the centre of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate:
- ∠DAB,
- ∠DBA,
- ∠DBC,
- ∠ADC.
Also, show that the ΔAOD is an equilateral triangle.
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
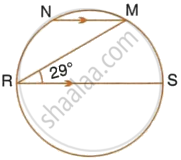
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠NRM
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBA
Also, show that the ΔAOD is an equilateral triangle.
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.