Advertisements
Advertisements
Question
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Solution
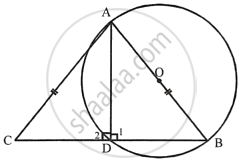
Given – In ∆ABC, AB = AC and a circle with AB as diameter is drawn
Which intersects the side BC and D.
To prove – D is the mid point of BC
Construction – Join AD.
Proof – ∠1 = 90° ...[Angle in a semi circle]
But ∠1 + ∠2 = 180° ...[Linear pair]
∴ ∠2 = 90°
Now in right ∆ABD and ∆ACD,
Hyp. AB = Hyp. AC ...[Given]
Side AD = AD ...[Common]
∴ By the right Angle – Hypotenuse – side criterion of congruence, we have
ΔABD ≅ ∆ACD ...[RHS criterion of congruence]
The corresponding parts of the congruent triangle are congruent.
∴ BD = DC ...[c.p.c.t]
Hence D is the mid point of BC.
APPEARS IN
RELATED QUESTIONS
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
Calculate the area of the shaded region, if the diameter of the semicircle is equal to 14 cm. Take `pi = 22/7`

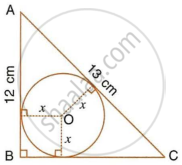
ABC is a right angles triangle with AB = 12 cm and AC = 13 cm. A circle, with centre O, has been inscribed inside the triangle.
Calculate the value of x, the radius of the inscribed circle.
Prove that the parallelogram, inscribed in a circle, is a rectangle.
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
- ∠DAB,
- ∠BDC.

The following figure shows a circle with PR as its diameter. If PQ = 7 cm and QR = 3RS = 6 cm, find the perimeter of the cyclic quadrilateral PQRS.
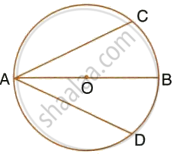
In the given figure, AB is the diameter of a circle with centre O.
If chord AC = chord AD, prove that:
- arc BC = arc DB
- AB is bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find:
- ∠BAC
- ∠ABC
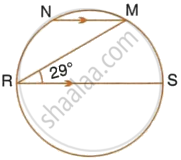
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠NRM
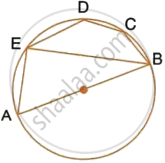
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate : ∠BCD.
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBA
Also, show that the ΔAOD is an equilateral triangle.