Advertisements
Advertisements
Question
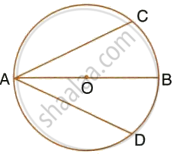
In the given figure, AB is the diameter of a circle with centre O.
If chord AC = chord AD, prove that:
- arc BC = arc DB
- AB is bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find:
- ∠BAC
- ∠ABC
Solution
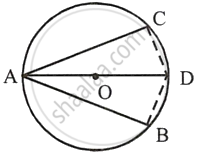
Given – In a circle with centre O, AB is the diameter and AC and AD are two chords such that AC = AD
To prove:
- arc BC = arc DB
- AB is the bisector of ∠CAD
- If arc AC = 2 arc BC, then find
- ∠BAC
- ∠ABC
Construction: Join BC and BD
Proof: In right angled ∆ABC and ∆ABD
Side AC = AD ...[Given]
Hyp. AB = AB ...[Common]
∴ By right Angle – Hypotenuse – Side criterion of congruence
ΔABC ≅ ΔABD
i. The corresponding parts of the congruent triangle are congruent.
∴ BC = BD ...[c.p.c.t]
∴ Arc BC = Arc BD ...[Equal chords have equal arcs]
ii. ∠BAC = ∠BAD
∴ AB is the bisector of ∠CAD
iii. If Arc AC = 2 arc BC,
Then ∠ABC = 2∠BAC
But ∠ABC + ∠BAC = 90°
`=>` 2∠BAC + ∠BAC = 90°
`=>` 3∠BAC = 90°
`=> ∠BAC = (90^circ)/3 = 30^circ`
∠ABC = 2∠BAC
`=>` ∠ABC = 2 × 30° = 60°
APPEARS IN
RELATED QUESTIONS
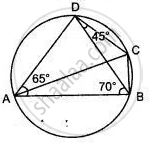
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
Prove that the parallelogram, inscribed in a circle, is a rectangle.
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°.
Calculate:
- ∠EBA,
- ∠BCD.
Prove that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
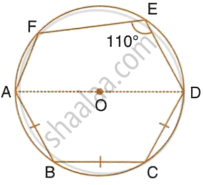
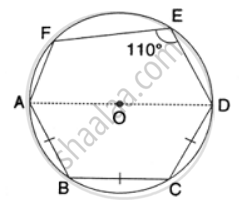
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate: ∠AEF
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠ADC
Also, show that the ΔAOD is an equilateral triangle.
In the following figure, AD is the diameter of the circle with centre O. chords AB, BC and CD are equal. If ∠DEF = 110°, Calculate: ∠FAB.
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.
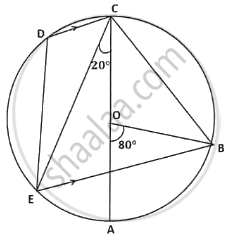
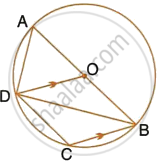
In the given figure AC is the diameter of the circle with centre O. CD is parallel to BE.
∠AOB = 80° and ∠ACE = 20°.
Calculate
- ∠BEC
- ∠BCD
- ∠CED