Advertisements
Advertisements
Question
Prove that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
Solution
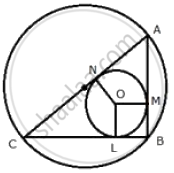
Join OL, OM and ON.
Let D and d be the diameter of the circumcircle and incircle.
And let R and r be the radius of the circumcircle and incircle.
In circumcircle of ΔABC,
∠B = 90°
Therefore, AC is the diameter of the circumcircle i.e. AC = D
Let radius of the incircle = r
∴ OL = OM = ON = r
Now, from B, BL, BM are the tangents to the incircle.
∴ BL = BM = r
Similarly,
AM = AN and CL = CN = R
(Tangents from the point outside the circle)
Now,
AB + BC + CA = AM + BM + BL + CL + CA
= AN + r + r + CN + CA
= AN + CN + 2r + CA
= AC + AC + 2r
= 2AC + 2r
= 2D + d
APPEARS IN
RELATED QUESTIONS
Prove that the parallelogram, inscribed in a circle, is a rectangle.
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
- ∠DAB,
- ∠BDC.

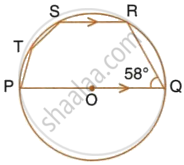
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°,
Calculate:
- ∠RPQ,
- ∠STP.
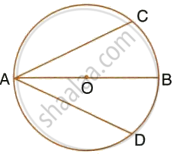
In the given figure, AB is the diameter of a circle with centre O.
If chord AC = chord AD, prove that:
- arc BC = arc DB
- AB is bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find:
- ∠BAC
- ∠ABC
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate : ∠BCD.
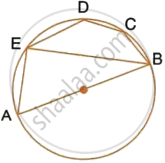
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBA
Also, show that the ΔAOD is an equilateral triangle.
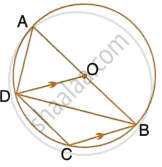
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBC
Also, show that the ΔAOD is an equilateral triangle.

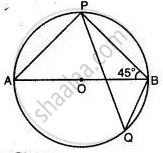
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.