Advertisements
Advertisements
Question
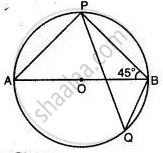
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.
Solution
Given ∠PBA = 45°
AOB is a diameter of circle.
∠APB = 90° ....(Angle in semi-circle)
So, in ΔAPB,
∠PAB = 180° - (90° + 45°) = 45°
∠PAB = ∠PQB ...(Angle in same segment)
∴ ∠PQB = 45°.
APPEARS IN
RELATED QUESTIONS
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
1) Prove that AC is a diameter of the circle.
2) Find ∠ACB
Prove that the rhombus, inscribed in a circle, is a square.
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
In the figure, given alongside, AB || CD and O is the centre of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate :
- ∠DAB,
- ∠BDC.

In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°.
Calculate:
- ∠EBA,
- ∠BCD.
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate:
- ∠DAB,
- ∠DBA,
- ∠DBC,
- ∠ADC.
Also, show that the ΔAOD is an equilateral triangle.
In the given figure, AB is the diameter of a circle with centre O.
If chord AC = chord AD, prove that:
- arc BC = arc DB
- AB is bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find:
- ∠BAC
- ∠ABC
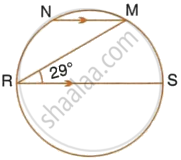
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠NRM
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate : ∠BCD.