Advertisements
Advertisements
प्रश्न
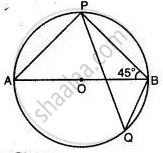
In the given figure, O is the centre of the circle and ∠PBA = 45°. Calculate the value of ∠PQB.
उत्तर
Given ∠PBA = 45°
AOB is a diameter of circle.
∠APB = 90° ....(Angle in semi-circle)
So, in ΔAPB,
∠PAB = 180° - (90° + 45°) = 45°
∠PAB = ∠PQB ...(Angle in same segment)
∴ ∠PQB = 45°.
APPEARS IN
संबंधित प्रश्न
In the figure, m∠DBC = 58°. BD is the diameter of the circle. Calculate:
1) m∠BDC
2) m∠BEC
3) m∠BAC
Prove that the parallelogram, inscribed in a circle, is a rectangle.
Prove that the rhombus, inscribed in a circle, is a square.
In the figure, given alongside, AB || CD and O is the centre of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
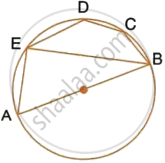
In the given figure, AB is the diameter of a circle with centre O.
If chord AC = chord AD, prove that:
- arc BC = arc DB
- AB is bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find:
- ∠BAC
- ∠ABC
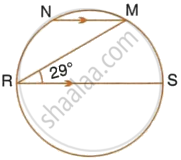
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠NRM
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate : ∠BCD.
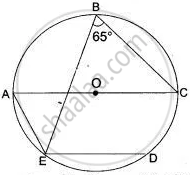
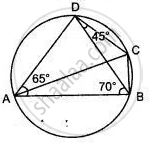
In the given figure, BAD = 65°, ABD = 70°, BDC = 45°.
(i) Prove that AC is a diameter of the circle.
(ii) Find ACB.
In Fig, Chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, Calculate ∠ DEC.