Advertisements
Advertisements
Question
A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.
Solution
Join BC. Let O be the centre of a circle. Join OA and OB
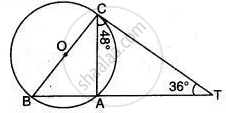
In Δ BCT, Δ ACT,
∠BTC = ∠ATC = 36°
∠ACT = ∠ABC = 48°
∴∠BAC = ∠ACT + ∠ATC
∠BAC = 48° + 36° = 84°
∴∠BCA = 180° - (∠ABC +∠BAC )
∠BCA = 180° - (48° + 84°) = 48°
∴∠BOA = 2∠BCA
∠BOA = 2 x 48° = 96°
APPEARS IN
RELATED QUESTIONS
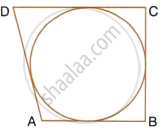
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
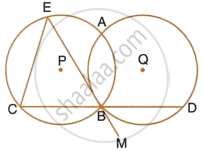
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
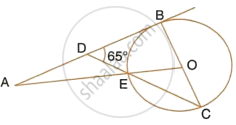
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
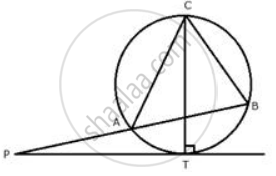
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
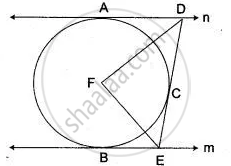
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
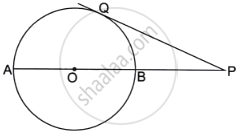
The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ: