Advertisements
Advertisements
Question
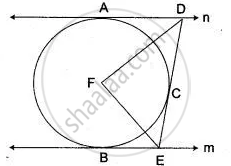
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
Solution
In triangles ADF and DFC, we have DA = DC ...(Tangents drawn from external point are equal in length)
DF = DF ...(Common)
AF = CF ...(Radii of the same circle)
So, by SSS-Criterion of congruence, we get
Δ ADF = ΔDFC
⇒ ∠ADF = ∠CDF
⇒ ∠ADC = 2∠CDF ...(i)
Similarly, we can prove that
∠BEF = ∠CEF
⇒ ∠CEB = 2∠CEF ....(ii)
Now, ∠ADC + ∠CEB = 180° ...(Sum of the interior angles on the same side of transversal is 180°)
⇒ 2(∠CDF + ∠CDF) = 180°
⇒ ∠CDF + ∠CEF = `(180°)/2`
⇒ ∠CDF + ∠CEF = 90°
Now, in ∠DEF,
⇒ ∠DFE + ∠CDF + ∠CEF = 180°
⇒ ∠DFE + 90° = 180°
⇒ ∠DFE = 180° - 90°
⇒ ∠DFE = 90°.
APPEARS IN
RELATED QUESTIONS
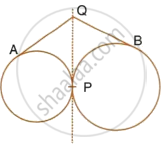
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
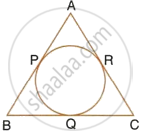
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
In the following figure; If AB = AC then prove that BQ = CQ.

In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ OQR
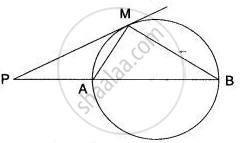
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2
A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.