Advertisements
Advertisements
प्रश्न
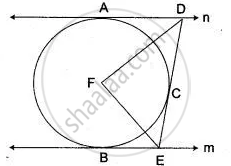
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
उत्तर
In triangles ADF and DFC, we have DA = DC ...(Tangents drawn from external point are equal in length)
DF = DF ...(Common)
AF = CF ...(Radii of the same circle)
So, by SSS-Criterion of congruence, we get
Δ ADF = ΔDFC
⇒ ∠ADF = ∠CDF
⇒ ∠ADC = 2∠CDF ...(i)
Similarly, we can prove that
∠BEF = ∠CEF
⇒ ∠CEB = 2∠CEF ....(ii)
Now, ∠ADC + ∠CEB = 180° ...(Sum of the interior angles on the same side of transversal is 180°)
⇒ 2(∠CDF + ∠CDF) = 180°
⇒ ∠CDF + ∠CEF = `(180°)/2`
⇒ ∠CDF + ∠CEF = 90°
Now, in ∠DEF,
⇒ ∠DFE + ∠CDF + ∠CEF = 180°
⇒ ∠DFE + 90° = 180°
⇒ ∠DFE = 180° - 90°
⇒ ∠DFE = 90°.
APPEARS IN
संबंधित प्रश्न
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
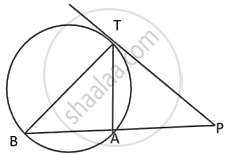
In the given figure, AB is the diameter of the circle, with centre O, and AT is the tangent. Calculate the numerical value of x.
In quadrilateral ABCD; angles D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm, Find the radius of the circle.
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
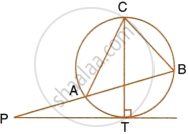
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

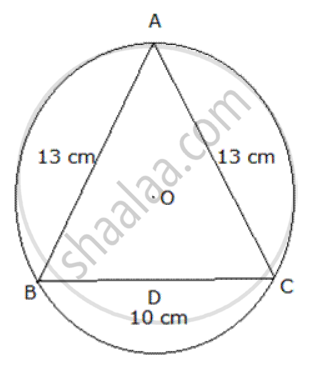
In figure , ABC is an isosceles triangle inscribed in a circle with centre O such that AB = AC = 13 cm and BC = 10 cm .Find the radius of the circle.
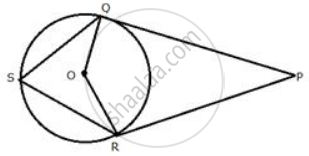
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ QSR
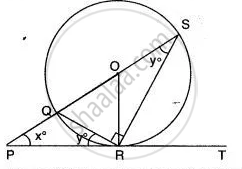
In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°
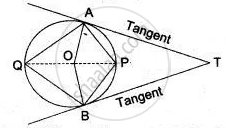
In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.