Advertisements
Advertisements
प्रश्न
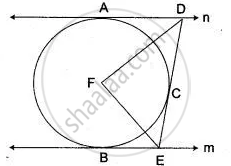
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
उत्तर
In triangles ADF and DFC, we have DA = DC ...(Tangents drawn from external point are equal in length)
DF = DF ...(Common)
AF = CF ...(Radii of the same circle)
So, by SSS-Criterion of congruence, we get
Δ ADF = ΔDFC
⇒ ∠ADF = ∠CDF
⇒ ∠ADC = 2∠CDF ...(i)
Similarly, we can prove that
∠BEF = ∠CEF
⇒ ∠CEB = 2∠CEF ....(ii)
Now, ∠ADC + ∠CEB = 180° ...(Sum of the interior angles on the same side of transversal is 180°)
⇒ 2(∠CDF + ∠CDF) = 180°
⇒ ∠CDF + ∠CEF = `(180°)/2`
⇒ ∠CDF + ∠CEF = 90°
Now, in ∠DEF,
⇒ ∠DFE + ∠CDF + ∠CEF = 180°
⇒ ∠DFE + 90° = 180°
⇒ ∠DFE = 180° - 90°
⇒ ∠DFE = 90°.
APPEARS IN
संबंधित प्रश्न
The radius of a circle is 8 cm. calculate the length of a tangent draw to this circle from a point at a distance of 10 cm from its centre.
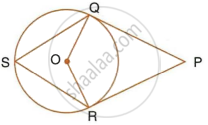
In the following figure; If AB = AC then prove that BQ = CQ.

Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
In the following figure, PQ and PR are tangents to the circle, with centre O. If `∠`QPR = 60°, calculate:
- ∠QOR,
- ∠OQR,
- ∠QSR.
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
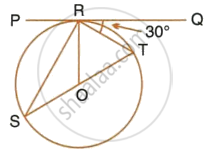
Given O is the centre of the circle and angle TRQ = 30°.
Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2