Advertisements
Advertisements
प्रश्न
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
उत्तर
Given: A circle with centre O touches the sides AB, BC, CD and DA of a quadrilateral ABCD at the points P, Q, R and S respectively.
To Prove: ∠ AOB + ∠ COD = 180° and ∠ AOD + ∠BOC = 180°.
Construction: Join OP, OQ, OR and OS.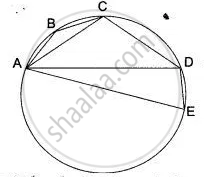
Proof: Since the two tangents drawn from an external point to a circle subtends equal angles at centre.
∴ ∠1 = ∠2, ∠3 = ∠4, ∠5 = ∠6 and ∠7 = ∠8 ...(i)
Now,
∠1 +∠2 +∠3 + ∠4 +∠5 +∠6 +∠7 +∠8 = 360° ...(Sum of all the angles subtended at a point is 360°)
⇒ 2(∠2 + ∠3 + ∠6 + ∠7) = 360° and 2(∠1 +∠8 + ∠4 +∠5) = 360°
⇒ (∠2 + ∠3) + (∠6 + ∠7) = 180° and (∠1 +∠8) + (∠4 +∠5) = 180°
⇒ ∠AOB + ∠COD = 180° ...(∵∠2 + ∠3 =∠AOB, ∠6 + ∠7 = ∠COD, ∠1 +∠8 = ∠AOD and ∠4 +∠5 = ∠BOC)
and ∠AOD + ∠BOC = 180°
APPEARS IN
संबंधित प्रश्न
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

In the following figure; If AB = AC then prove that BQ = CQ.

In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
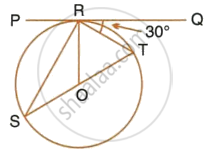
Given O is the centre of the circle and angle TRQ = 30°.
AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

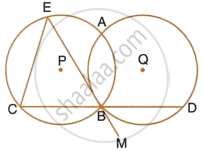
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
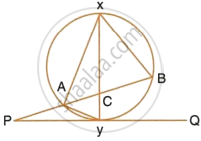
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

