Advertisements
Advertisements
प्रश्न
Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

उत्तर
Given: Two equal chords AB and CD intersecting at a point E.
To prove: BE = BE and AE = CE
Construction: Join OE. Draw OL ⊥ AB and OM ⊥ CD'
Proof: We have
AB = CD
⇒ OL = OM ....(∵Equal chords are equidistant from the centre)
In triangles OLE and OME, we have
OL = OM
∠OLE = ∠OME ...(Each equal to 90°)
and OE = OE ...(Common)
So, by SAS-Criterion of congruences
Δ OLE ≅ ΔOME
⇒ LE = ME ....(i)
Now, AB = CD
⇒ `1/2"AB" = 1/2"CD"` ⇒ BL = DM ...(ii)
Subtracting (ii) from (i), we get
LE - BL = ME - DM
⇒ BE = DE
Again, AB = CD and BE = DE
⇒ AB + BE = CD + DE
⇒ AE = CE
Hence, BE = DE and AE = CE.
Hence proved.
APPEARS IN
संबंधित प्रश्न
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

A line intersecting a circle in two points is called a ______.
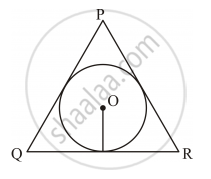
In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
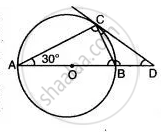
In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
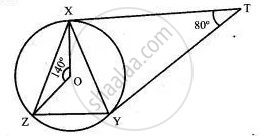
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
The distance between two parallel tangents of a circle of radius 4 cm is ______
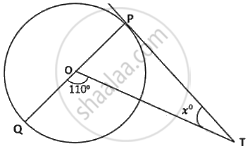
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.