Question

In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

Answer 1

Since ΔPQR is a right-angled angle,

PR = `sqrt(7^2 + 24^2) = sqrt(49 + 576) = sqrt625 = 25 cm`

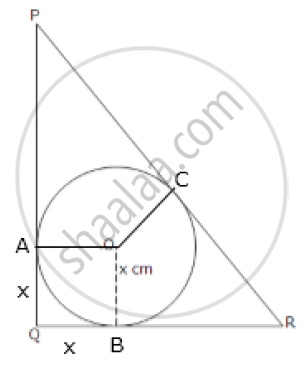
Let the given inscribed circle touches the sides of the given triangle at points A, B and C respectively.

Then, clearly, OAQB is a square.

=> AQ = BQ = x cm

PA = PQ – AQ = (24 – x) cm

RB = QR – BQ = (7 – x) cm

Since tangents from an exterior point to a circle are equal,

PC = PA = (24 – x) cm

And, RC = RB = (7 – x) cm

PR = PC + CR

=> 25 = (24 – x) + (7 – x)

=> 25 = 31 – 2x

=> 2x = 6

=> x = 3 cm

Hence, the radius of the inscribed circle is 3 cm.

Answer 2

OM ⊥ QR
ON ⊥ PQ     ....( Tangents and radius perpendicular to each other.)
OM = ON = r
QM = QN    ....( Tangents from an external point)

⇒ QMON is a square.
⇒ QM = OM = ON = QN = x cm

So, mR = (7 - x) cm
PN = (24 - x) cm
PT = PN = 24 - x
and, mR = RT = 7 - x       ....(Tangents from an external point)

⇒ PR = PT + RT
PR = 24 - x + 7 - x 
PR = 31 - 2x

Now, In ΔPQR,
PR² = PQ² + QR²
PR² = 24² + 7²
PR² = 576 + 49 = 625
PR = 25 cm

⇒ 31 - 2x = 25
⇒ 2x = 31 - 25
⇒ 2x = 6
⇒ x = 3.