Advertisements
Advertisements
प्रश्न
In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

उत्तर १
Since ΔPQR is a right-angled angle,
PR = `sqrt(7^2 + 24^2) = sqrt(49 + 576) = sqrt625 = 25 cm`
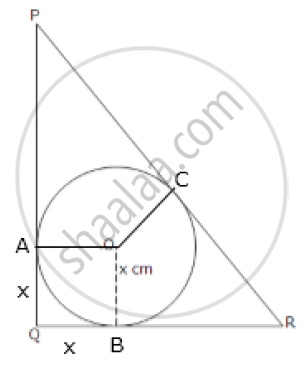
Let the given inscribed circle touches the sides of the given triangle at points A, B and C respectively.
Then, clearly, OAQB is a square.
=> AQ = BQ = x cm
PA = PQ – AQ = (24 – x) cm
RB = QR – BQ = (7 – x) cm
Since tangents from an exterior point to a circle are equal,
PC = PA = (24 – x) cm
And, RC = RB = (7 – x) cm
PR = PC + CR
=> 25 = (24 – x) + (7 – x)
=> 25 = 31 – 2x
=> 2x = 6
=> x = 3 cm
Hence, the radius of the inscribed circle is 3 cm.
उत्तर २
OM ⊥ QR
ON ⊥ PQ ....( Tangents and radius perpendicular to each other.)
OM = ON = r
QM = QN ....( Tangents from an external point)

⇒ QMON is a square.
⇒ QM = OM = ON = QN = x cm
So, mR = (7 - x) cm
PN = (24 - x) cm
PT = PN = 24 - x
and, mR = RT = 7 - x ....(Tangents from an external point)
⇒ PR = PT + RT
PR = 24 - x + 7 - x
PR = 31 - 2x
Now, In ΔPQR,
PR2 = PQ2 + QR2
PR2 = 242 + 72
PR2 = 576 + 49 = 625
PR = 25 cm
⇒ 31 - 2x = 25
⇒ 2x = 31 - 25
⇒ 2x = 6
⇒ x = 3.
APPEARS IN
संबंधित प्रश्न
How many common tangents can be drawn to two circles, touching each
other externally?
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
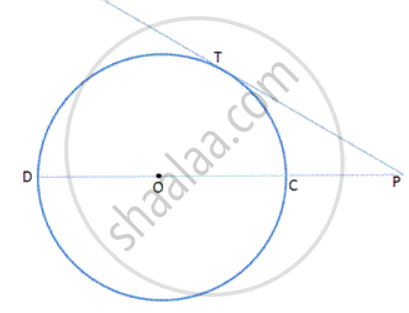
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

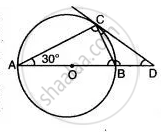
In Figure, AB is diameter and AC is a chord of a circle such that ∠BAC = 30°. The tangent at C intersects AB produced at D. Prove that BC = BD.
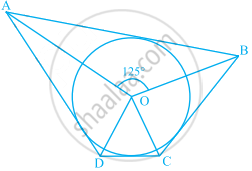
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
The tangents drawn at the extremities of the diameter of a circle are ______.

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
