Advertisements
Advertisements
प्रश्न
How many common tangents can be drawn to two circles, touching each
other externally?
पर्याय
One
Two
Three
Four
उत्तर
Three
APPEARS IN
संबंधित प्रश्न
A line intersecting a circle in two points is called a ______.
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
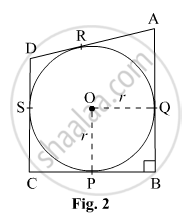
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
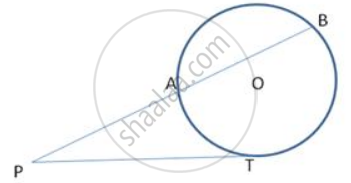
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
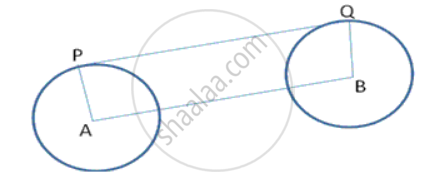
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ALOB is a cyclic quadrilateral.
Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

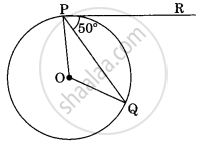
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
Tangents from an external point to a circle are ______
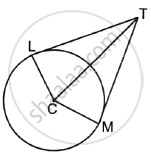
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.
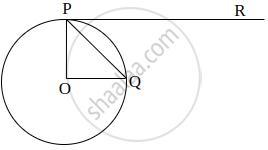
If O is centre of a circle and Chord PQ makes an angle 50° with the tangent PR at the point of contact P, then the angle subtended by the chord at the centre is ______.
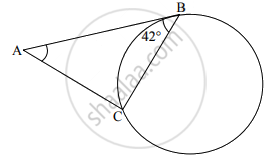
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
