Advertisements
Advertisements
प्रश्न
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
उत्तर
PQ is tangent to circle OM is perpendicular PQ chord AC and ∠COM = 65°
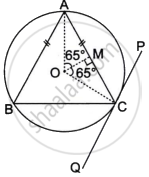
a. Here, ∠AOM = ∠COM = 65°
= 65° + 65°
= 130°
Now, ∠ABC = `1/2` ∠AOC ...(Since, angle at the centre is twice the angle formed by the same arc at any other point of the circle)
= `1/2 xx 130^circ`
= 65°
b. In ΔABC,
AB = AC
∠ABC = ∠ACB = 65° ...(Since, angles opposite to equal sides are equal)
∴ ∠BAC = 180° – (65° + 65°)
= 180° – 130°
= 50°
c. ∠OCQ = 90° ...(Since, angle between the radius and the tangent is 90°)
In ΔOMC,
∠OCM = 180° – (∠OMC + ∠MOC) ...[By angle sum property of triangle]
= 180° – (90° + 65°)
= 180° – 155°
= 25°
∠ACB = 65°
∠OCB = ∠ACB – ∠OCM
= 65° – 25°
= 40°
∠BCQ = ∠OCQ – ∠OCB
= 90° – 40°
= 50°
APPEARS IN
संबंधित प्रश्न
The common point of a tangent to a circle and the circle is called ______.
In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
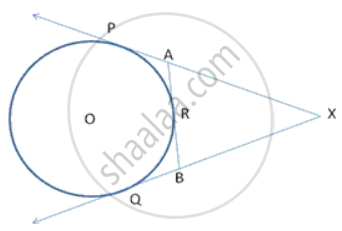
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

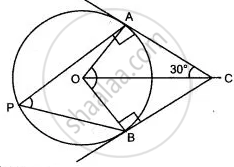
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
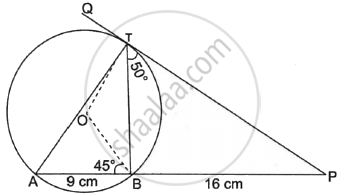
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT
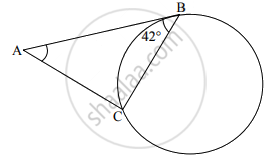
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
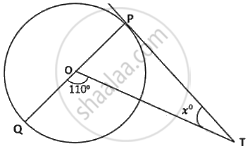
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.