Advertisements
Advertisements
प्रश्न
In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
उत्तर
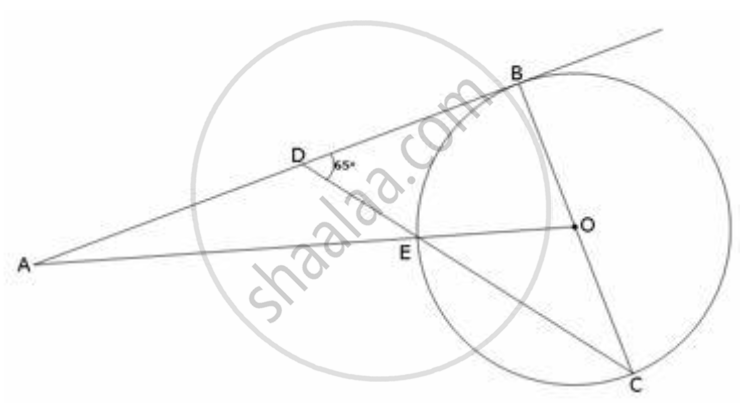
Form the given figure OB is the radius and therefore in triangle BDC
`∠DBC + ∠BDC + ∠BCD = 180^@`
`=> 90^@ + 65^@ + ∠BCD = 180^@`
=> ∠BCD = 25
Now, OE = OC = radius, ∠OEC = ∠OCE = 25° (as ∠OCE = ∠BCD)
=> ∠AED = ∠OEC = 25° (Vertically opposite angles)
Also, `∠ADE = 180^@ - 65^@ = 115^@`
Therefore in triangle AED
`∠BAO = 180^@ - 115^@ - 25^@ = 40^@`
APPEARS IN
संबंधित प्रश्न
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
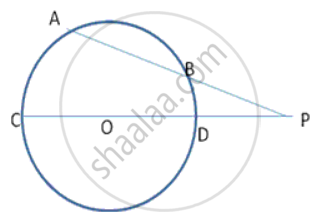
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
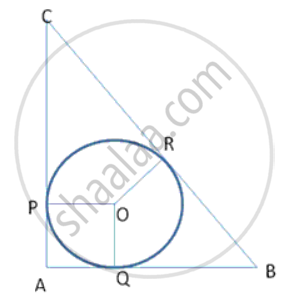
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

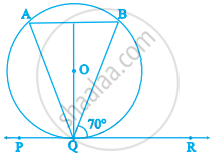
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to ______.
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

