Advertisements
Advertisements
प्रश्न
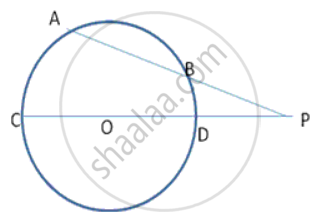
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
उत्तर
Let OD = OC = r (say)
PO = 14.5 , CP = r + 14.5
PD = 14.5 - r
In Δ BPD and Δ APC
∠ BPD = ∠ APC {Common)
∠ ABD + ∠ DBP = 180° ---(1) ( Linear pair )
Also, ∠ ABD + ∠ ACD = 180° ---(2} {Opposite angles of a cyclic quadrilateral)
From (1) and {2}
∠ DBP = ∠ ACD
∴ Δ BPD ~ Δ CPA {AA corollary)
`8/("r" + 14.5) = (4.5 - "r")/15`
120° = 14.52 - r2
r2 = 210.25- 120
r2 = 90.25
r = 9.50
Radius of the circle is 9.5cm .
APPEARS IN
संबंधित प्रश्न
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
How many tangents can a circle have?
A line intersecting a circle in two points is called a ______.

In the figure, point Q is the
point of contact. If PQ = 12,
PR = 8 then find PS.
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
The length of the direct common tangent to two circles of radii 12cm and 4cm is 15cm. calculate the distance between their centres.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

If O is centre of a circle and Chord PQ makes an angle 50° with the tangent PR at the point of contact P, then the angle subtended by the chord at the centre is ______.