Advertisements
Advertisements
Question
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
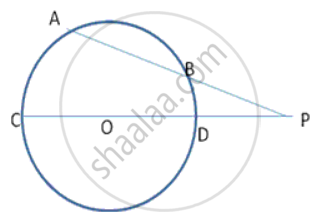
Solution
Let OD = OC = r (say)
PO = 14.5 , CP = r + 14.5
PD = 14.5 - r
In Δ BPD and Δ APC
∠ BPD = ∠ APC {Common)
∠ ABD + ∠ DBP = 180° ---(1) ( Linear pair )
Also, ∠ ABD + ∠ ACD = 180° ---(2} {Opposite angles of a cyclic quadrilateral)
From (1) and {2}
∠ DBP = ∠ ACD
∴ Δ BPD ~ Δ CPA {AA corollary)
`8/("r" + 14.5) = (4.5 - "r")/15`
120° = 14.52 - r2
r2 = 210.25- 120
r2 = 90.25
r = 9.50
Radius of the circle is 9.5cm .
APPEARS IN
RELATED QUESTIONS
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
In the given figure, find TP if AT = 16 cm and AB = 12 cm.

Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
The length of the direct common tangent to two circles of radii 12cm and 4cm is 15cm. calculate the distance between their centres.
A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?
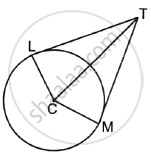
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

