Advertisements
Advertisements
Question
The length of the direct common tangent to two circles of radii 12cm and 4cm is 15cm. calculate the distance between their centres.
Solution
R1 = 4cm, R2 = 12cm
PQ = l5 cm
AB2 = PQ2 + (R2 - R1)2
=> AB2 = 152 + (12 - 4)2
=> AB2 = 225 + 64
=>AB2 = 289
=> AB = 17cm
The diameter between the centre is 17cm
APPEARS IN
RELATED QUESTIONS
How many tangents can a circle have?
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.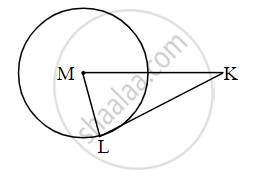
A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?
Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

