Advertisements
Advertisements
Question
Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
Solution

Steps of construction:
- Draw a circle with radius 4 cm with the centre as O.
- Take a point A on the circumference of the circle and join OA.
- Draw a radius OB, making an angle of 120° (180° – 60°) with OA.
- Draw a perpendicular to OB at point B and perpendicular to OA at point A. Let both perpendiculars intersect at point P.
PA and PB are the required tangents at an angle of 60°.
APPEARS IN
RELATED QUESTIONS
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
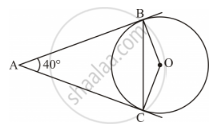
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
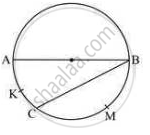
In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is ______
