Advertisements
Advertisements
Question
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is ______
Options
4 cm
5 cm
6 cm
8 cm
Solution
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is 8 cm.
Explanation:
First, draw a circle of radius 5 cm with centre O.
A tangent XY is drawn at point A.
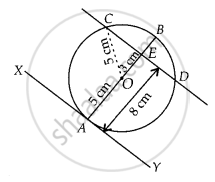
A chord CD is drawn which is parallel to XY and at a distance of 8 cm from A.
Now, ∠OAY = 90° ...[∵ Tangent at any point of circle is perpendicular to the radius through the point of contact]
∠OAY + ∠OED = 180° ...[∵ Sum of cointerior angles is 180°]
⇒ ∠OED = 180° – 90° = 90°
Also, AE = 8 cm.
Join OC
OC = 5 cm ...[Radius of circle]
OE = AE – OA
= 8 – 5
= 3 cm
Now, in right angled ∆OEC,
OC2 = OE2 + EC2 ...[By Pythagoras theorem]
⇒ EC2 = OC2 – OE2
⇒ EC2 = 52 – 32
⇒ EC2 = 25 – 9 = 16
⇒ EC = 4 cm
Since, perpendicular from centre to the chord bisects the chord.
∴ CE = ED
⇒ CD = 2 × EC
⇒ CD = 2 × 4
⇒ CD = 8 cm
APPEARS IN
RELATED QUESTIONS
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
The distance between two parallel tangents of a circle of radius 4 cm is ______
Tangents from an external point to a circle are ______
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
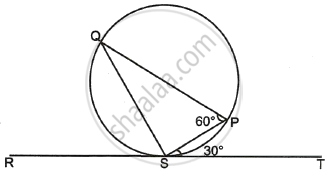
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.