Advertisements
Advertisements
Question
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
Solution
Let QR be a chord in a circle with center O and ∠1 and ∠2 are the angles made by tangent at point R and Q with chord respectively.
To Prove: ∠1 = ∠2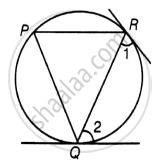
Let P be another point on the circle, then, join PQ and PR.
Since, at point Q, there is a tangent.
∠RPQ = ∠2 ...[Angles in alternate segments are equal] [Equation 1]
Since, at point R, there is a tangent.
∠RPQ = ∠1 ...[Angles in alternate segments are equal] [Equation 2]
From equation 1 and equation 2
∠1 = ∠2
Hence Proved.
APPEARS IN
RELATED QUESTIONS
The common point of a tangent to a circle and the circle is called ______.
In the given figure, find TP if AT = 16 cm and AB = 12 cm.

In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

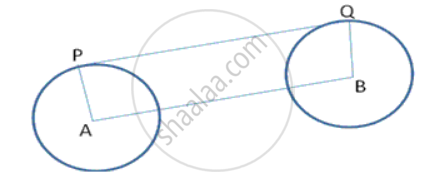
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
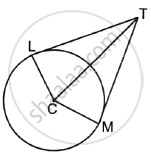
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______

If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

