Advertisements
Advertisements
Question
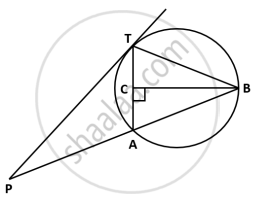
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

Solution
In order to prove that ΔADT is isosceles i.e., TA = TD, it is sufficient to show that ∠TAD = ∠TDA.
Since ∠TAB and ∠BCA are angles in the alternate segments of chord AB.
∴ ∠TAB = ∠BCA ...(i)
It is given that AD is the bisector of ∠BAC.
∠BAD = ∠CAD ...(ii)
Now, ∠TAD = ∠TAB + ∠BAD
⇒ ∠TAD = ∠BCA + ∠CAD ....(Using (i) and (ii))
⇒ ∠TAD = ∠DCA + ∠CAD ....( ∵∠BCA = ∠DCA)
⇒ ∠TAD = 180° - ∠CAD ....( In ΔCAD, ∠CAD + ∠DCA +∠CDA = 180° ∴ ∠CAD + ∠BCA = 180° - ∠CAD)
⇒ ∠TAD = ∠TDA ....(∵∠CDA + ∠TDA = 180°)
= TD = TA
Hence, ΔADT is isosceles
Hence proved.
APPEARS IN
RELATED QUESTIONS
In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
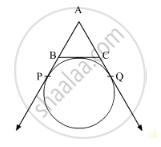

In the figure, point Q is the
point of contact. If PQ = 12,
PR = 8 then find PS.
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
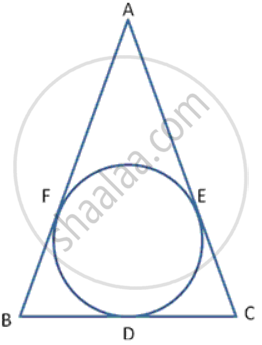
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
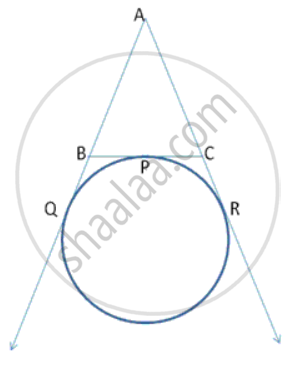
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT