Advertisements
Advertisements
Question
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
Solution
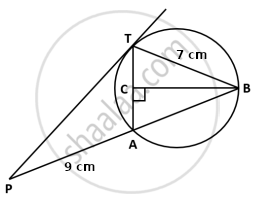
Given: In diagram PT is tangent BC bisects TA at right angles.
BT = 7 cm, PA = 9 cm
(a) Line segment BC is a common side of both the ΔACB and ΔTCB.
ΔACB is 90° then ΔTCB also is 90°.
Hence the length of BT and the length of AB will be the same.
∴ Length of BT is 7 cm then length of AB is also 7 cm.
(b) PT2 = PA × PB
PT2 = 9 × (9 + 7)
PT2 = 9 × 16
PT = `sqrt(9 xx 16)`
PT = 3 × 4
PT = 4 cm
APPEARS IN
RELATED QUESTIONS

In the figure, point Q is the
point of contact. If PQ = 12,
PR = 8 then find PS.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
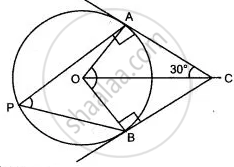
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
