Advertisements
Advertisements
Question
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Solution
Given, AB is a diameter of the circle.
A tangent is drawn from point A.
Draw a chord CD parallel to the tangent MAN.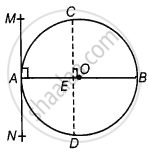
So, CD is a chord of the circle and OA is a radius of the circle.
∴ ∠MAO = 90° ...[Tangent at any point of a circle is perpendicular to the radius through the point of contact]
⇒ ∠CEO = ∠MAO ...[Corresponding angles]
∴ ∠CEO = 90°
Thus, OE bisects CD, ...[Perpendicular from centre of circle to chord bisects the chord]
Similarly, diameter AB bisects all chords which are parallel to the tangent at the point A.
APPEARS IN
RELATED QUESTIONS
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)


In the figure, point Q is the
point of contact. If PQ = 12,
PR = 8 then find PS.
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
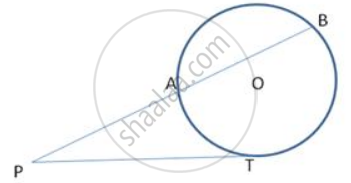
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
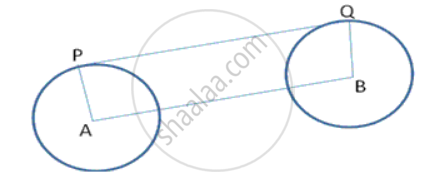
The tangents drawn at the extremities of the diameter of a circle are ______.
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
