Advertisements
Advertisements
Question
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
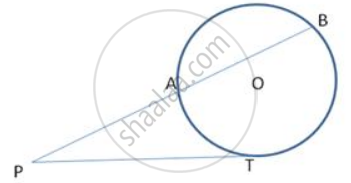
Solution
Given AP and AQ are diameters of circles with centre O and O1 respectively
∴ ∠ APB = 90° ---( 1) (Angle in a semidrde is a right angle)
Similarly, ∠ ABQ = 90° ---(2)
Adding (1) and (2)
∠ APB + ∠ ABQ = 90° + 90°
∠ PBQ = 180°
Hence, PBQ is a straight line
∴ P, B and Q are collinear.
APPEARS IN
RELATED QUESTIONS
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
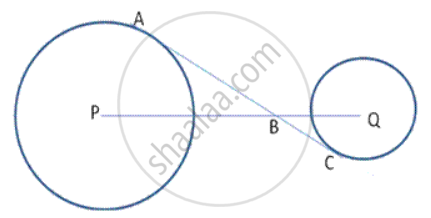
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
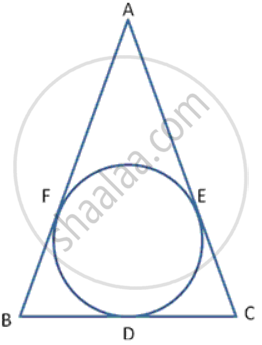
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

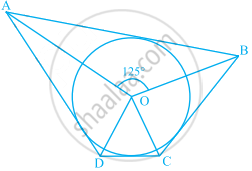
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.