Advertisements
Advertisements
Question
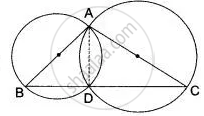
Two circles are drawn with sides AB, AC of a triangle ABC as diameters. They intersect at a point D. Prove that D lies on BC.
Solution 1
AB and AC are diameters of circles with oentre O and O1 respectively
∠ ADB = 90 ° ---( 1) (Angle in a semi circle is a right angle)
Similarly, ∠ ADB = 90° ---(2)
Adding ( 1) and (2)
∠ ADB + ∠ ADC = 90 + 90
∠ BDC = 180°
Hence, BDC is a straight line.
Solution 2
Join AD.
Since angle in a semi-circle is a right angle.
Therefore,
∠ADB = 90° and ∠ADC = 90°
⇒ ∠ADB + ∠ADC = 90° + 90°
⇒ ∠ADB + ∠ADC = 180°
BDC is a straight line.
⇒ D lies on BC.
Hence proved.
APPEARS IN
RELATED QUESTIONS
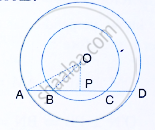
In the following figure, AD is a straight line. OP ⊥ AD and O is the centre of both the circles. If OA = 34 cm. OB = 20 cm and OP = 16cm; find the length of AB.
The length of common chord of two intersecting circles is 30 cm. If the diameters of these two circles be 50 cm and 34 cm, calculate the distance between their centres.
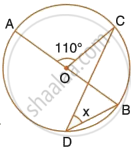
In the figure, given alongside, AOB is a diameter of the circle and ∠AOC = 110°. Find ∠BDC.
In the figure, chords AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm; find DE.
In the figure, AB is the chord of a circle with centre O and DOC is a line segment such that BC = DO. If ∠C = 20°, find angle AOD.

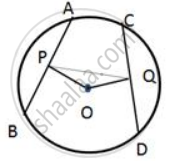
In the given figure, QAP is the tangent at point A and PBD is a straight line.
If ∠ACB = 36° and ∠APB = 42°, find:
- ∠BAP
- ∠ABD
- ∠QAD
- ∠BCD
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.
If ∠CAB = 34°, Find : ∠CBA
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In following figure . O is the centre of the circle. Find ∠ BAC.
In the given figure, AB and CD are two equal chords of a circle, with centre O. If P is the mid-point of chord AB, Q is the mid-point of chord CD and ∠POQ = 150°, find ∠APQ.