Advertisements
Advertisements
Question
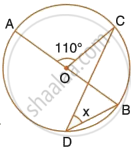
In the figure, given alongside, AOB is a diameter of the circle and ∠AOC = 110°. Find ∠BDC.
Solution

Join AD.
Here, `∠ADC = 1/2 ∠AOC`
= `1/2xx 110^circ`
= 55°
(Angle at the centre is double the angle at the circumference subtended by the same chord)
Also, ∠ADB = 90°
(Angle in a semicircle is a right angle)
∴ ∠BDC = 90° – ∠ADC
= 90° – 55°
= 35°
APPEARS IN
RELATED QUESTIONS
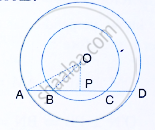
In the following figure, AD is a straight line. OP ⊥ AD and O is the centre of both the circles. If OA = 34 cm. OB = 20 cm and OP = 16cm; find the length of AB.
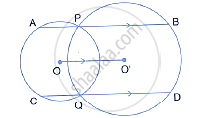
In the following figure; P and Q are the points of intersection of two circles with centres O and O’. If straight lines APB and CQD are parallel to O O'; prove that:
(i) O O' = `1/2AB` (ii) AB = CD
The diameter and a chord of a circle have a common end-point. If the length of the diameter is 20 cm and the length of the chord is 12 cm, how far is the chord from the centre of the circle?
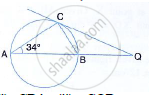
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q.
If ∠CAB = 34°, Find : ∠CBA
Prove that the line segment joining the midpoints of two parallel chords of a circle passes through its centre.
Two circles are drawn with sides AB, AC of a triangle ABC as diameters. They intersect at a point D. Prove that D lies on BC.
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
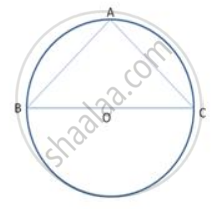
In following figure . O is the centre of the circle. Find ∠ BAC.
In following figure , chord ED is parallel to the diameter AC of the circle. Given ∠ CBE = 65° , calculate ∠DEC .
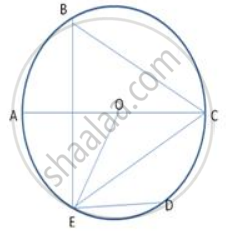
In the given figure, AB and CD are two equal chords of a circle, with centre O. If P is the mid-point of chord AB, Q is the mid-point of chord CD and ∠POQ = 150°, find ∠APQ.