Advertisements
Advertisements
Question
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

Solution
Let ABC be the right angled triangle such that ∠B = 90° , BC = 6 cm, AB = 8 cm. Let O be the centre and r be the radius of the incircle.
AB, BC and CA are tangents to the circle at P, N and M.
∴ OP = ON = OM = r (radius of the circle)
By Pythagoras theorem,
CA2 = AB2 + BC2
⇒ CA2 = 82 + 62
⇒ CA2 = 100
⇒ CA = 10 cm
Area of ∆ABC = Area ∆OAB + Area ∆OBC + Area ∆OCA
APPEARS IN
RELATED QUESTIONS
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

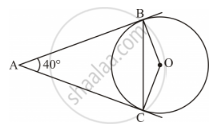
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
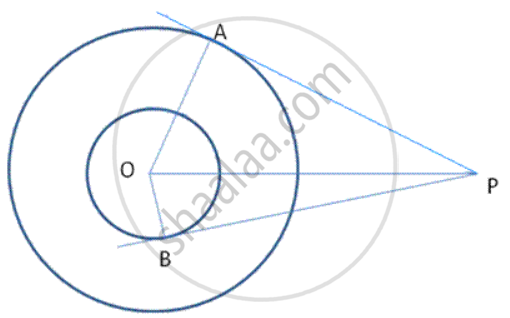
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
Two parallel lines touch the circle at
points A and B respectively. If the area of the circle is 25 n cm2, then AB is equal to ______
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.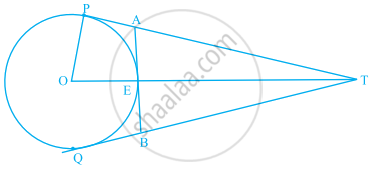
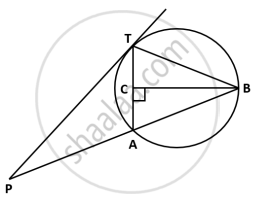
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
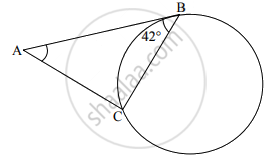
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
