Advertisements
Advertisements
Question
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
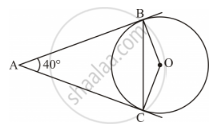
Options
40°
50°
140°
150°
Solution
It is known that the tangent is perpendicular to the radius through the point of contact.
∴ ∠ABO = ∠ACO = 90°
Using angle sum property in quadrilateral ABOC:
∠ABO + ∠BOC + ∠ACO + ∠BAC = 360°
⇒ 90° + ∠BOC + 90° + 40° = 360°
⇒ ∠BOC + 220° = 360°
⇒ ∠BOC = 360° - 220° = 140°
APPEARS IN
RELATED QUESTIONS
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle APB

In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

The quadrilateral formed by joining the angle bisectors of a cyclic quadrilateral is a ______
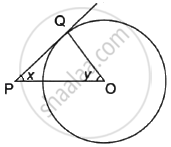
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
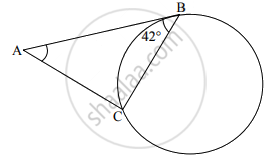
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
