Advertisements
Advertisements
Question
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
Options
A. 8 a
B. 4 a
C. 2 a
D. 16 a
Solution
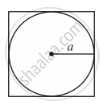
The radius of the circle is given as a cm.
∴ Diameter of the circle = 2 × a cm = 2a cm
Side of the circumscribing square = Diameter of the circle = 2a cm
Perimeter of the circumscribing square = 4 × 2a cm = 8a cm
APPEARS IN
RELATED QUESTIONS
From an external point P, tangents PA and PB are drawn to the circle with centre O. If CD is the tangent to the circle at point E and PA = 14 cm. Find the perimeter of ABCD.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
In the given figure, O is the centre of the circle. Find ∠CBD.

In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?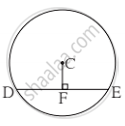
If O is the center of the circle in the figure alongside, then complete the table from the given information.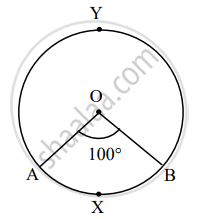
The type of arc
| Type of circular arc | Name of circular arc | Measure of circular arc |
| Minor arc | ||
| Major arc |
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c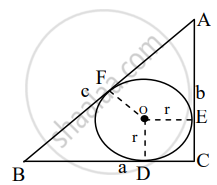
From the figure, identify a segment.

