Advertisements
Advertisements
Question
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
Solution
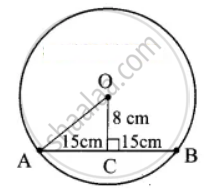
Distance AC = `1/2 xx "Length of chord"`
= `1/2 xx 30`
= 15 cm
Distance from the centre = 8 cm
In ΔOAC Radius (OA) = `sqrt("AC"^2 + "OC"^2)`
= `sqrt(15^2 + 8^2)`
= `sqrt(225 + 64)`
= `sqrt(289)`
= 17
Radius of the circle = 17 cm.
APPEARS IN
RELATED QUESTIONS
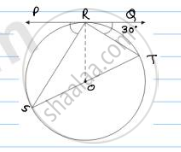
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
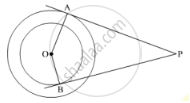
From an external point P, tangents PA and PB are drawn to a circle with center O. If CD is the tangent to the circle at a point E and PA = 14cm, find the perimeter of ΔPCD.

Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

Draw circle with diameter: 8.4 cm
In above case, measure the length of the radius of the circle drawn.
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
AD is a diameter of a circle and AB is a chord If AD = 30 cm and AB = 24 cm then the distance of AB from the centre of the circle is
Twice the radius is ________________
A, B, C are any points on the circle with centre O. If m(arc BC) = 110° and m(arc AB) = 125°, find measure arc AC.