Advertisements
Advertisements
Question
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
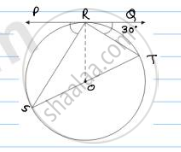
Solution
Given ∠TRQ = 30°.
At point R, OR ⊥ RQ.
∠ORQ = 90°
⇒ ∠TRQ + ∠ORT = 90°
⇒ ∠ORT = 90° − 30° = 60°
ST is diameter, ∠SRT = 90° [∵ Angle in semicircle = 90°]
∠ORT + ∠ SRO = 90°
∠SRO + ∠PRS = 90°
∠PRS = 90° − 30° = 60°
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
In figure OQ : PQ = 3 : 4 and perimeter of ΔPDQ = 60cm. determine PQ, QR and OP.
Prove that two different circles cannot intersect each other at more than two points.
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
Circles with centres A, B and C touch each other externally. If AB = 36, BC = 32, CA = 30, then find the radii of each circle.
Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
Is every diameter of a circle also a chord?
