Advertisements
Advertisements
Question
Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at center.
Solution
Consider circle with center ‘O’ and has two parallel tangents through A & B at ends of
diameter.
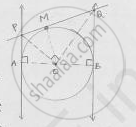
Let tangents through M intersects the tangents parallel at P and Q required to prove is that ∠POQ = 90°.
From fig. it is clear that ABQP is a quadrilateral
∠A + ∠B = 90° + 90° = 180° [At point of contact tangent & radius are perpendicular]
∠A + ∠B + ∠P + ∠Q = 360° [Angle sum property]
∠P + ∠Q = 360°−180° = 180° …..(i)
At P & Q ∠APO = ∠OPQ =1/2∠𝑃
∠BQO = ∠PQO =`1/2`∠𝑄 in (i)
2∠OPQ + 2 ∠PQO = 180°
∠OPQ + ∠PQO = 90° …. (ii)
In ΔOPQ, ∠OPQ + ∠PQO + ∠POQ = 180° [Angle sum property]
90° + ∠POQ = 180° [from (ii)]
∠POQ = 180° − 90° = 90°
∴ ∠POQ = 90°
APPEARS IN
RELATED QUESTIONS
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
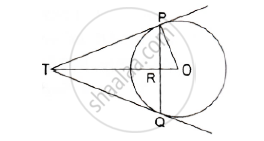
PQ is a chord of length 4.8 cm of a circle of radius 3cm. The tangents at P and Q intersect at a point T as shown in the figure. Find the length of TP.
A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
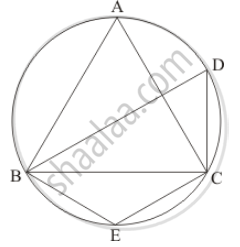
In the given figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.
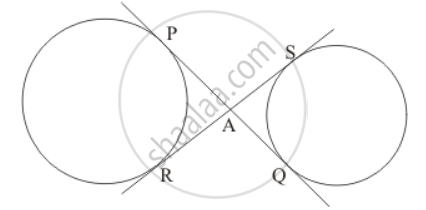
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
The circumcentre of a triangle is the point which is ______.
