Advertisements
Advertisements
Question
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
Solution
Perimeter of ΔAPQ, (P) = AP + AQ + PQ
= AP + AQ + (PX + QX)
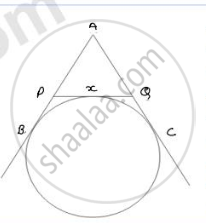
We know that
The two tangents drawn from external point to the circle are equal in length from point A,
AB = AC = 5 cm
From point P, PX = PB
From point Q, QX = QC
Perimeter (P) = AP + AQ + (PB + QC)
= (AP + PB) + (AQ + QC)
= AB + AC = 5 + 5
= 10 cms.
APPEARS IN
RELATED QUESTIONS
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle, is bisected at the point of contact.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In the given figure, PA and PB are the tangent segemtns to a circle with centre O. Show that he points A, O, B and P are concyclic.

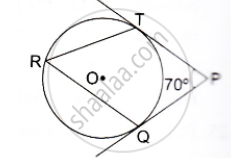
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
In the following figure, if AOB is a diameter and ∠ADC = 120°, then ∠CAB = 30°.