Advertisements
Advertisements
Question
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
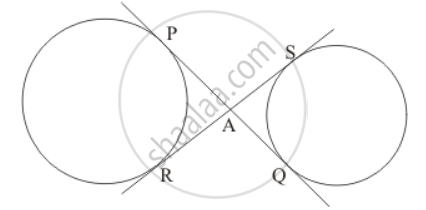
Solution
The figure given in the question is
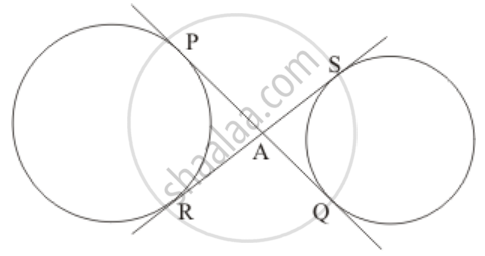
We know from the property of tangents that the length of two tangents drawn from a common external point will be equal. Therefore,
PA = RA …… (1)
AQ = AS …… (2)
Let us add equation (1) and (2)
PA + AQ = RA + AS
PQ = RS
Thus we have proved that PQ = RS.
APPEARS IN
RELATED QUESTIONS
In fig., O is the centre of the circle, PA and PB are tangent segments. Show that the quadrilateral AOBP is cyclic.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
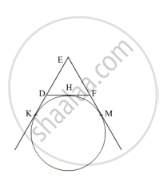
In Fig 2, a circle touches the side DF of ΔEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ΔEDF (in cm) is:
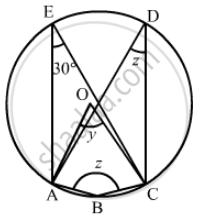
In the given figure, O is the centre of the circle. If ∠CEA = 30°, Find the values of x, y and z.
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
State, if the following statement is true or false:
Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
Is every diameter of a circle also a chord?
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
