Advertisements
Advertisements
Question
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
Solution
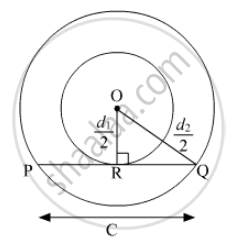
Let O be the centre of two concentric circles and PQ be the tangent to the inner circle that touches the circle at R.
Now, OQ= \[\frac{1}{2} d_2\] and
OR=\[\frac{1}{2} d_1\]
Also, PQ = c
As, PQ is the tangent to the circle.
⇒ OR ⊥ PQ
⇒ QR =\[\frac{1}{2}PQ = \frac{1}{2}c\]
In Triangle OQR,
∴ By Pythagoras Theorem,
\[\left( OQ \right)^2 = \left( OR \right)^2 + \left( RQ \right)^2 \]
\[ \Rightarrow \left( \frac{d_2}{2} \right)^2 = \left( \frac{d_1}{2} \right)^2 + \left( \frac{c}{2} \right)^2 \]
\[ \Rightarrow \left( d_2 \right)^2 = \left( d_1 \right)^2 + c^2\]
APPEARS IN
RELATED QUESTIONS
In Fig., if AB = AC, prove that BE = EC
Fill in the blank:
A point whose distance from the centre of a circle is greater than its radius lies in ..................... of the circle.
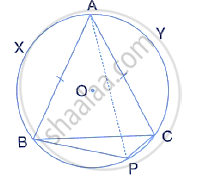
In the given figure ABC is an isosceles triangle and O is the centre of its circumcircle. Prove that AP bisects angle BPC .
In the given figure, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that point of contact P bisects the base BC.

In a cyclic quadrilateral ABCD, if m ∠A = 3 (m ∠C). Find m ∠A.
Use the figure given below to fill in the blank:
Tangent to a circle is _______.

A line through the point of contact and passing through centre of the circle is known as ______
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
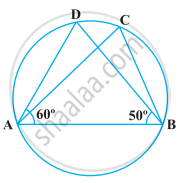
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
Draw two acute angles and one obtuse angle without using a protractor. Estimate the measures of the angles. Measure them with the help of a protractor and see how much accurate is your estimate
