Advertisements
Advertisements
Question
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

Solution
Let us join the point of contact E with the centre of the circle say O. Also, let us join the point of contact F with the centre of the circle O. Now we have a quadrilateral AEOF.
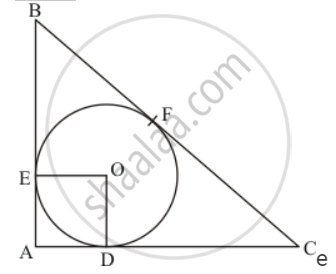
In this quadrilateral we have,
`∠EAD = 90^0`(Given in the problem)
`∠oda = 90^0`(Since the radius will always be perpendicular to the tangent at the point of contact)
`∠OEA = 90^0`(Since the radius will always be perpendicular to the tangent at the point of contact)
We know that the sum of all angles of a quadrilateral will be equal to `360^o`. Therefore,
`∠EAD + ∠ ODA + ∠ EOD + ∠ OEA = 360^o`
`90^0+90^o +90^o + ∠EOD = 360^o`
` ∠EOD = 90^o`
Since all the angles of the quadrilateral are equal to 90° and the adjacent sides are equal, this quadrilateral is a square. Therefore all the sides are equal. We have found that
AF = 5
Therefore,
OD = 5
OD is nothing but the radius of the circle.
Thus we have found that AF = 5 cm and radius of the circle is 5 cm.
APPEARS IN
RELATED QUESTIONS
A tangent to a circle intersects it in ______ point (s).
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

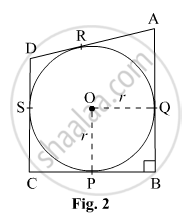
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
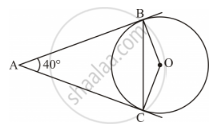
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB